What is a Delta?
This is the ratio that compares change in price of a derivative to the change in price of the underlying assets. It is equally known as the age ratio. Delta is a risk sensitive guideline adopted in testing derivatives. It is one of the numerous guideline and is represented by a Greek letter. The arrays of risk messages that make use of such letters are closely regarded to as the Greeks. They are also known as health parameters risk measures or risk sensitivities. Among the Greek delta is one of the most crucial metrics.
How to interpret Delta?
General explaination
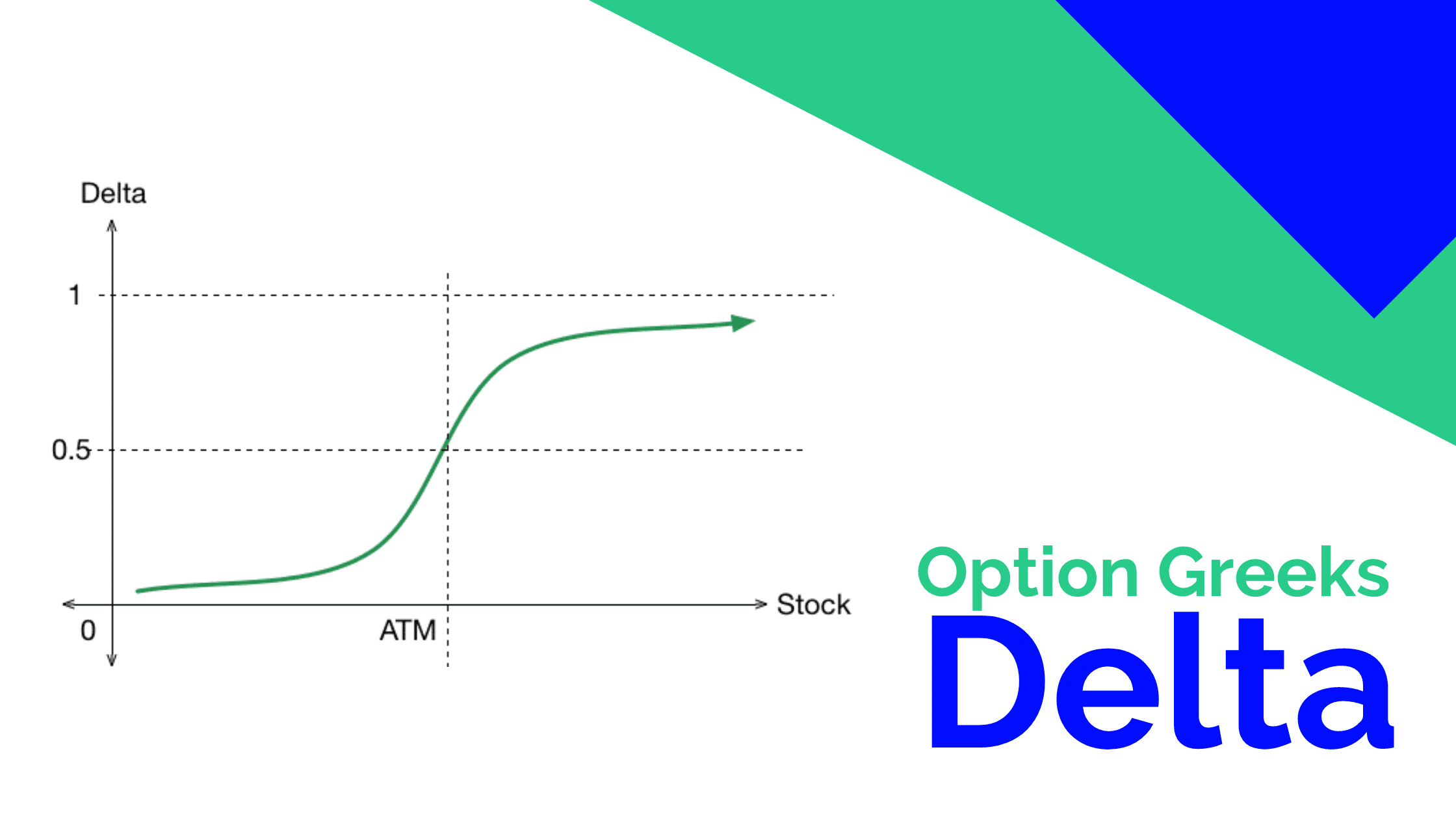
The delta ratio can be positive or negative. This is determined by the direction the derivative takes in relation to changes in the underlying asset. A call option will increase in value and thereby having a positive delta. Conversely, a put option would decrease in value when the underlying asset rises in price. Thereby it has a negative delta. For a call option the value would range from 0 to 1. For a put option value would range from 0 to -1.
Examples of this ratio
Let’s say a call option has a value of $10 and the underlying asset as a $20 price. Then the underlying asset price increases 2 $23 and option value corresponds by increasing to $11. The delta is equal to:
($11 – $10) / ($23 – $20) = 0.33
Now let’s examine a put option with a value of $10. The underlying asset as $20 price and decreases to $17. The corresponding put option value increases to $11. The delta here is equal to:
($11 – $10) / ($17 – $20) = -0.33
Another way of imagining the metric is that it can give an idea of probably an option will up in the money at the expiration date. As an option goes further into the money, the delta value will move away from 0. For a call option it will move towards a value of 1 while a put option will move towards a value of -1. As the option moves further out of the money the delta value will move towards 0. The delta is 0.50 when a call option is at the money and -0.50 for a put option when it is at the money. This means the strike price is equal to the underlying asset price.
It is basically implying that there is a 50/50 chance of the auction ending in the money or out of the money. The delta sensitivity is also affected by the time until expiration. The closer the option is to the expiration the more certainly for option to end up in its current state. It is either in or out or at the money. If a call option is in the money holding the moneyless constant as it nears expiration, the delta figure will move near, towards 1.
What is Delta used for?
- Traders may put into consideration the sensitivity value as the amount of their exposure to a stock or the underlying asset. The nearest value is 21 the more the vulnerable they are to the underlying asset full.
- The Delta value of an option can also be used as a means to verify if the options has sold or bought. If the price of an option rises less than the delta, it could mean that Traders are selling this auction close to the bid price. If the bid prices is higher than the Delta would imply, it may indicate that Traders were buying the options near the ask price
- Delta can also be used for hedging sake. A famous hedging strategy in use is the neutral delta strategy. It includes holding a number of option which when the delta is taken in aggregate it is equivalent or really near to 0. This reduces the movement in option pricing relative to the underlying price asset.
What are option Greeks?
Option Greeks are financial measures of the sensitivity of an options price to its underlying determining parameters. These parameters are volatility or the price of underlying asset. The Greeks are used in the analysis of an options portfolio. They also are key in sensitivity analysis of an option or portfolio of options. The measures are regarded important by many Traders for making reasonable decisions in options trading. Some examples of key option Greeks are: Delta, Gamma, Vega Theta and Rho. There are many other option Greeks that can be generated from the aforementioned ones.
Putting options delta to use
There are basically two major means by which a trader can use delta. It is imperative to remember though that this value is only an indication of how the price of an option is likely to change. It is not an assurance of how it will change.
Profitability estimate
The primary use of Delta is to provide you with an idea of how much money you will make if the underlying stock moves as you predicted it to or how much you will lose if the underlying stock moves in an opposite direction of your prediction. This can assist you to decide which options give you the best value for money. This is in regards of benefiting from what you predicted.
For example, you might believe that stock in company ‘A’ is going to increase in price by a certain amount over a specific time period. By observing the delta values of the relevant calls with different strike prices you can try to work out how to maximize your likely profits or minimize your likely losses.
Probability estimate
The second main use is based on probability. The delta value of an option can be used to determine the approximate probability of it expiring in the money. The closer the delta value is to 0, the less chance it has of finishing in the money. Conversely, call options with a delta value close to 1 and puts options with a value close to -1, have a very high opportunity of finishing in the money. Although the calculations involved in delta and not exactly associated 2 probability in this sense it’s still a logical way to gauge the rough probability of an option expiring in the money.
As a result this can help you determine which trades to make. It let’s you weigh up the risks involved in a trade against the strength of your prediction. It is based on what will happen to the relevant underlying stock. Delta values can be used to place targets for your trades. It helps traders determine at what point you should end a trade and take your profits or cut your losses.
Example of Delta
- Let us presume there is a publicly traded corporation called GeeCorps. Shares of its stock are bought and sold on a stock exchange. And there are put options and call options traded for those shares. The delta for the call option on GeeCorp shares. The delta for the call option on GeeCorp shares is 0.25. That means that a $1 change in the price of GeeCorp stock generates a $0.25 change in the price of GeeCorp call options. Thus, if GeeCorp’s shares trade at $30 and the call option trades at $2, a change in the price of GeeCorp’s shares to $31 means the call option will increase to a price of $2.25.
- Put options works in the opposite way. If the put option on GeeCorp shares has a delta of -$0.55, then a $1 increase in GeeCorp’s share price generates a $0.55 decrease in the price of GeeCorp’s put options. So if GeeCorp’s share trade at $10 and the put option trades at $2, then GeeCorp’s shares increase to $11, and the put option will decrease to a price of $1.45.
Conclusion
An option with huge delta will move in price rapidly in ratio to the price movements of the underlying security while one with small Delta will move less often. The most popular tool for carrying out a delta spread strategy is a calendar spread. It includes constructing a Delta neutral position using options with diverse expiration dates. It can be positive or negative appearing between 0 and 1 for a call option and -1 and 0 for a put option.
 Good Trading requires the Best Charting Tool!
Good Trading requires the Best Charting Tool!
 We loved Marwood Research’s course “Candlestick Analysis For Professional Traders“. Do you want to follow a great video course and deep dive into 26 candlestick patterns (and compare their success rates)? Then make sure to check this course!
We loved Marwood Research’s course “Candlestick Analysis For Professional Traders“. Do you want to follow a great video course and deep dive into 26 candlestick patterns (and compare their success rates)? Then make sure to check this course!